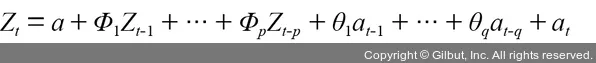질문 양식
이름
질문내용
7. 시계열 분석
7.1 시계열 문제
시계열 분석 : 시간에 따라 변하는 데이터를 사용하여 추이를 분석하는 것. 즉, 추세를 파악하거나 향후 전망등을 예측하기 위한 용도로 사용
시계열 형태(the components of time series)는 데이터 변동 유형에 따라 불규칙 변동, 추세 변동, 순환 변동, 계절 변동으로 구분할 수 있습니다.
•
불규칙 변동(irregular variation): 시계열 자료에서 시간에 따른 규칙적인 움직임과 달리 어떤 규칙성이 없어 예측 불가능하고 우연적으로 발생하는 변동을 의미합니다. 전쟁, 홍수, 화재, 지진, 파업 등이 대표적인 예입니다.
•
추세 변동(trend variation): 시계열 자료가 갖는 장기적인 변화 추세를 의미합니다. 이때 추세란 장기간에 걸쳐 지속적으로 증가·감소하거나 또는 일정한 상태(stationary)를 유지하려는 성향을 의미하기 때문에 짧은 기간 동안에는 추세 변동을 찾기 어려운 단점이 있습니다. 추세 변동의 대표적인 예로는 국내총생산(GDP), 인구증가율 등이 있습니다.
•
순환 변동(cyclical variation): 대체로 2~3년 정도의 일정한 기간을 주기로 순환적으로 나타나는 변동을 의미합니다. 즉, 1년 이내 주기로 곡선을 그리며 추세 변동에 따라 변동하는 것으로, 경기 변동이 대표적입니다.
•
계절 변동(seasonal variation): 시계열 자료에서 보통 계절적 영향과 사회적 관습에 따라 1년 주기로 발생하는 것을 의미합니다. 보통 계절에 따라 순환하며 변동하는 특성이 있습니다.
7.2 AR, MA, ARMA, ARIMA
시계열 분석은 독립 변수(independent variable)를 사용하여 종속 변수(dependent variable)를 예측하는 일반적인 머신 러닝에서 시간을 독립 변수로 사용한다는 특징이 있다.
7.2.1. AR 모델
AR(AutoRegressive)(자기 회귀) : 이전 관측 값이 이후 관측 값에 영향을 준다는 아이디어에 대한 모형으로 자기 회귀 모델이라고도 한다.
①은 시계열 데이터에서 현재 시점을 의미하며, ②는 과거가 현재에 미치는 영향을 나타내는 모수(Φ)에 시계열 데이터의 과거 시점을 곱한 것입니다. 마지막으로 ③은 시계열 분석에서 오차 항을 의미하며 백색 잡음이라고도 합니다. 따라서 수식은 p 시점을 기준으로 그 이전의 데이터에 의해 현재 시점의 데이터가 영향을 받는 모형이다.
② 과거가 현재에 미치는 영향을 나타내는 모수(Φ)에 시계열 데이터의 과거 시점을 곱하여 구한다.
③ 시계열 분석에서 오차 항을 의미하며 백색 잡음이라고도 합니다.
따라서 수식은 p 시점을 기준으로 그 이전의 데이터에 의해 현재 시점의 데이터가 영향을 받는 모형이다.
7.2.2. MA 모델
MA( Moving Average)(이동 평균) : 트렌드(평균 혹은 시계열 그래프에서 y 값)가 변화하는 상황에 적합한 회귀 모델이다.
기계열을 따라서 윈도우 크기만큼 슬라이딩된다고 하여 이동 평균 모델이라고 한다.
①은 시계열 데이터에서 현재 시점을 의미하며, ②는 매개변수(θ)에 과거 시점의 오차를 곱한 것입니다. 마지막으로 ③은 오차 항을 의미합니다. 따라서 수식은 AR 모델처럼 이전 데이터의 ‘상태’에서 현재 데이터의 상태를 추론하는 것이 아닌, 이전 데이터의 오차에서 현재 데이터의 상태를 추론하겠다는 의미이다.
② 매개변수(θ)에 과거 시점의 오차를 곱하여 구한다.
③ 오차 항을 의미
따라서 수식은 AR 모델처럼 이전 데이터의 ‘상태’에서 현재 데이터의 상태를 추론하는 것이 아닌,
이전 데이터의 오차에서 현재 데이터의 상태를 추론하겠다는 의미이다.
7.2.3 ARMA 모델
ARMA( AutoRegressive Moving Average)(자기 회귀 이동 평균) : AR과 MA를 섞은 모델로 연구 기관에서 주로 사용
ARIMA( AutoRegressive Integrated Moving Average)(자기 회귀 누적 이동 평균) : 자기 회귀와 이동 평균을 둘 다 고려하는 모형인데, ARMA와 달리 과거 데이터의 선형 관계뿐만 아니라 추세(cointegration)까지 고려한 모델
7.2.4. ARIMA 모델
statsmodels 라이브러리를 이용하여 ARIMA 모델을 구현할 수 있다.
1.
ARIMA(p,d,q) 함수를 호출하여 사용하며 p는 자기 회귀 차수, b는 차분 차수, q는 이동 평균 차수
2.
fit() 메서드를 호출하고 모델에 데이터를 적용하여 훈련
3.
predict() 메서드를 호출하여 미래의 추세 및 동향에 대해 예측한다.
AR모형의 Lag을 의미하는 p, MA모형의 Lag(시계열)을 의미하는 q, 차분(Diffrence)횟수를 의미하는 d 가 그것이다. 보통은 p, d, q의 순서로 쓴다.통상적으로 p + q < 2, p * q = 0 인 값들을 많이 사용한다.
여기서 p * q = 0 이라 하면, 두 값중 하나는 0이라는 이야기이다. ARIMA는 AR모형과 MA모형을 하나로 합쳤다면서 둘 중 하나의 모수가 0인건 또 무슨소리? 라고 할지 모르겠지만, 실제로 대부분의 시계열 자료에서는 하나의 경향만을 강하게 띄기 때문에, 이렇게 사용하는것이 더 잘 맞는다고 한다.
from pandas import read_csv
from pandas import datetime
from pandas import DataFrame
from statsmodels.tsa.arima_model import ARIMA
from matplotlib import pyplot
def parser(x):
return datetime.strptime('199'+x, '%Y-%m')#%Y-%m날짜와 시간 정보>문자열
series = read_csv('/content/sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
model = ARIMA(series, order=(5,1,0))
model_fit = model.fit(disp=0)#disp=0 모형을 적용할 때 많은 디버그 정보가 제공되는데 disp 인수를 0으로 설정하여 비활성화한다.
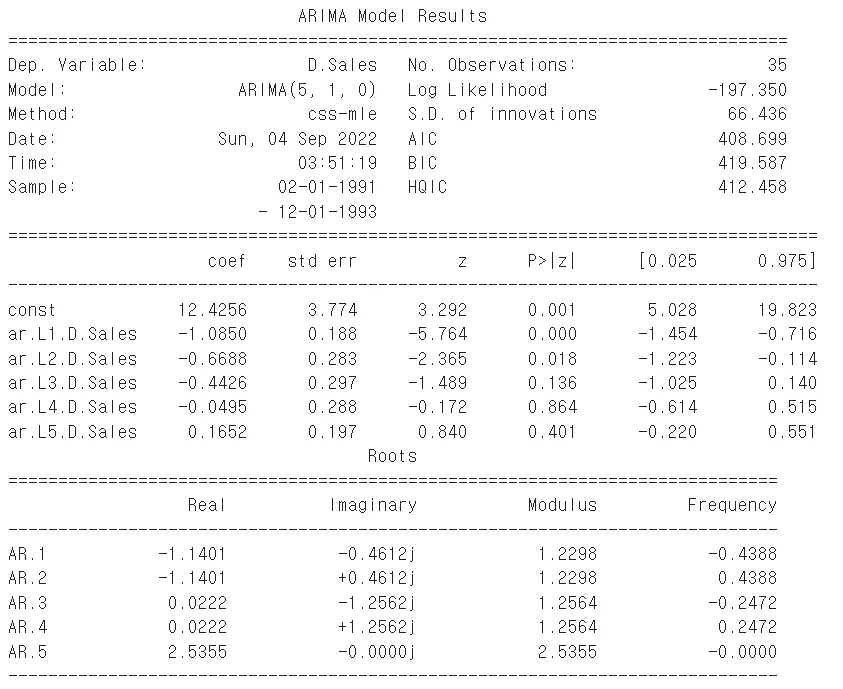
print(model_fit.summary())
residuals = DataFrame(model_fit.resid)#오차정보저장
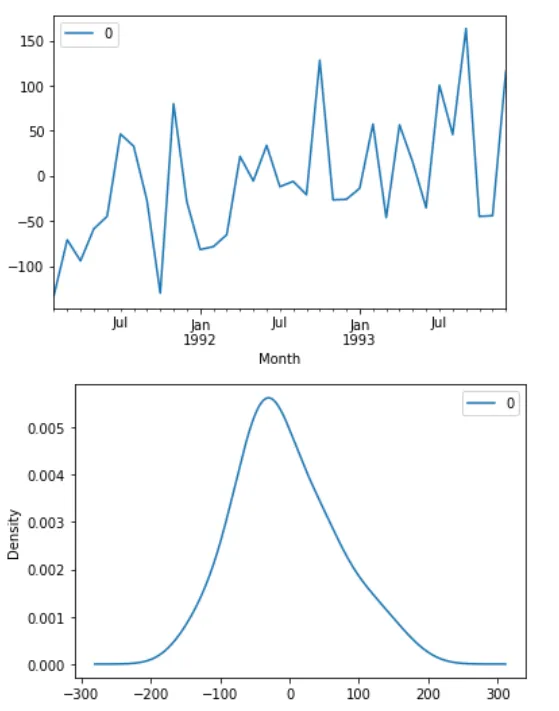
residuals.plot()
pyplot.show()
residuals.plot(kind='kde')
pyplot.show()
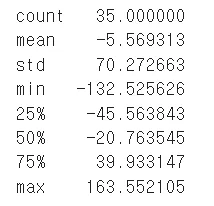
print(residuals.describe())
Python
복사
오차정보(위), 예제의 밀도 정보(아래)
ARIMA() 함수를 사용하여 예측을 하면
import numpy as np
from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
from statsmodels.tsa.arima_model import ARIMA
from sklearn.metrics import mean_squared_error
def parser(x):
return datetime.strptime('199'+x, '%Y-%m')
series = read_csv('/content/sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
X = series.values
X = np.nan_to_num(X)
size = int(len(X) * 0.66)
train, test = X[0:size], X[size:len(X)] #트레이닝과 테스트로 분리
history = [x for x in train]
predictions = list()
for t in range(len(test)): #테스트 데이터셋 길이(13)만큼만 출력)
model = ARIMA(history, order=(5,1,0))
model_fit = model.fit(disp=0)
output = model_fit.forecast()#forecast() 메서드로 예측
yhat = output[0] #결과는 yhat에 저장
predictions.append(yhat)#predictions에 결과값을 리스트로 저장
obs = test[t]
history.append(obs)
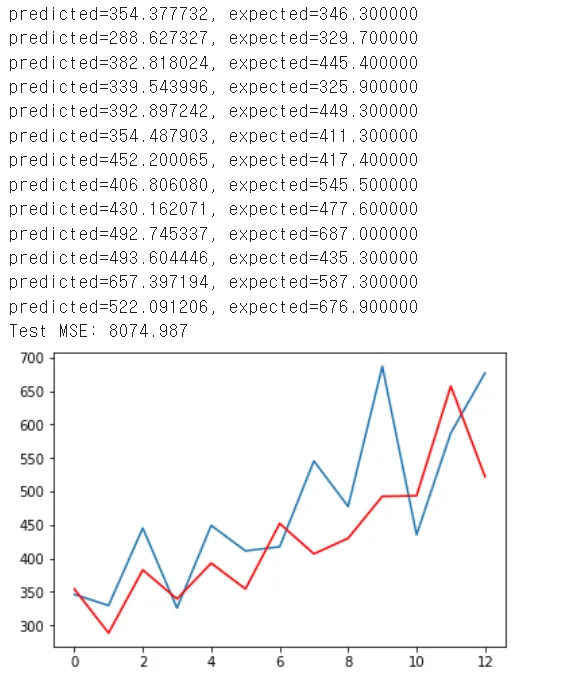
print('predicted=%f, expected=%f' % (yhat, obs))
error = mean_squared_error(test, predictions) #손실함수는 평균제곱오차
print('Test MSE: %.3f' % error)
pyplot.plot(test)
pyplot.plot(predictions, color='red')#저장된 결과값을 그래프로 출력
pyplot.show()
Python
복사
실제데이터(빨강)과 모형 실행 결과(파랑)를 표시한 그래프가 출력된다.